Question Block 1
Unsure what we're asking? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Can my student read and write numerals from 0 to 9?
Does my student have one-to-one correspondence (e.g., the numeral 7 represents seven objects)?
Do I think my student is ready to start formal instruction?
Question Block 2
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Question Block 3
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Can my student explain how regrouping (a.k.a. "carrying" or "borrowing") works using the language of place value?
If they solved 147 + 385 using only a pencil and paper, would they be able to explain why they wrote a "1" above the "4"?
(i.e. "When there are more than 9 in the units or ones place, 10 of them have to be regrouped as 1 ten in the tens place")
Question Block 4
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Does my student understand multiplication in terms of repeated addition and in geometric (i.e. rectangular area) terms?
Would they be able to express 3 × 4 as 3 + 3 + 3 + 3 (repeated addition)?
Would they also be able to identify the multiplication problem this rectangle (3 × 4 geometric area) represents?

Question Block 5
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Question Block 6
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Question Block 7
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Question Block 8
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Question Block 9
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Question Block 10
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Question Block 11
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
Can my student use discriminants and an understanding of the quadratic formula to predict the nature of the solutions to a quadratic equation?
Would they be able to predict whether the roots to 7x2 − 3x = 20 will be real or complex, rational or irrational, and equal or unequal without using a calculator or solving the equation?
Question Block 12
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".
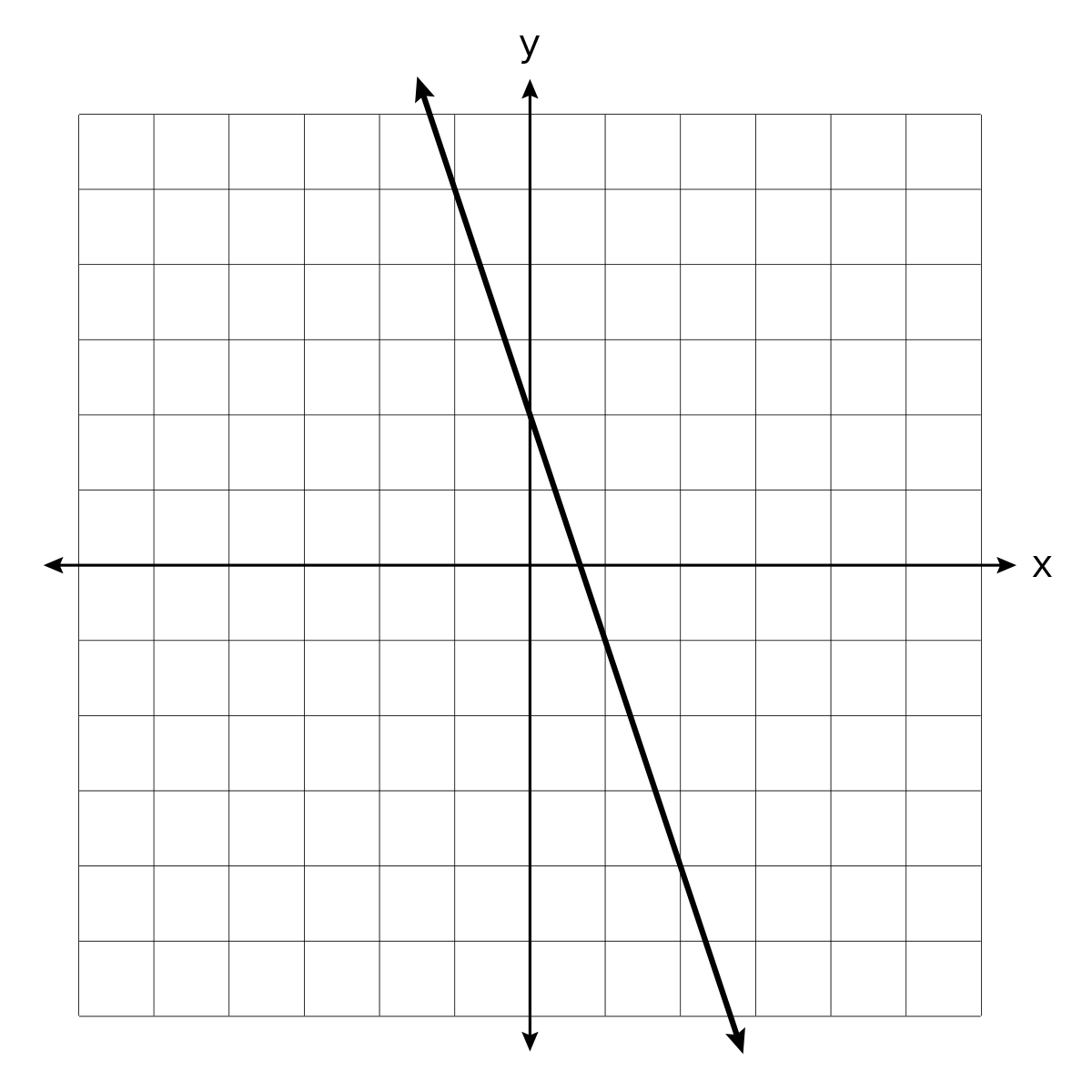
Can my student identify parts of a quadratic function responsible for translation, direction, and amplitude?
Given y = −2x2 + 4x + 3, would they be able to predict that the graph will be a parabola, that the negative sign indicates that the vertex will be at the top of the curve, and that the curve will be steeper than the curve for y = −x2?
Can my student identify parts of a trigonometric function responsible for amplitude, translation, and period?
Given y = 2sin(4x) + 3, would they be able to predict that the 2 indicates the amplitude, that the 3 indicates the vertical translation, and would they be able to use the 4 to find the period ?
Question Block 13
Unsure what we're asking? Click "Show Example" to see what we're talking about. Still not sure? No problem. Select "Unsure" and we'll give you a couple of questions in a Quick Check guide to work through with your student so you can select "Yes" or "Not Yet".